2021虎符CTF-Cubic密码题解

这次做这道椭圆曲线的密码的原因是之前见过这个有趣的方程问题。这题求方程：

$$\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}=6$$

约束条件：

• x,y,z 都是正整数，并且六组解都互素，即给了约束条件gcd（x,y,z）=1,也就是不能由一组解简单构造多解。
• 不计x,y,z的顺序，即不能简单得由一组解排列组合。

上面这个方程要爆破到第一组最小的解是不可能的。毕竟这个方程看起来简单（整数解确实简单），但是它的最小正整数解有足足150位！最小解如下：

x=20260869859883222379931520298326390700152988332214525711323500132179943287700005601210288797153868533207131302477269470450828233936557
y=1218343242702905855792264237868803223073090298310121297526752830558323845503910071851999217959704024280699759290559009162035102974023
z=2250324022012683866886426461942494811141200084921223218461967377588564477616220767789632257358521952443049813799712386367623925971447

如果要爆算的话，假设最优的只要穷举两个数，那么至少数量级为10^300。现在顶尖的超算也不超过10^20每秒，那么穷举时间大概是10^280s,这个数字应该比宇宙的年龄都大多了。

后面第六组解到了4500位（应该是最小的前六组解了），这个看似简单的方程的解就是如此离谱。

这个题我之前看过zml大佬的博客，有点印象，就把博客翻出来看了一下。有兴趣看详细数学原理的移步大佬的博客以及一篇14年的论文An unusual cubic representation problem(可见这个问题早些年求解出来是可以发数论方向的论文的)，我后面写的东西偏脚本一些。

（呜呜，然而因为第一次碰到nc交互因为输入过长被截断的情况，让我一度怀疑题目错了，错过了拿flag的时间，后面拿socket交互在服务器没关的时候还是拿了flag，还是比赛经验太少了，雾）
 
 

服务器源码

#!/usr/bin/env python3
from math import gcd
from functools import reduce
from fractions import Fraction as Frac

N = 6

def read_num(prompt):
    try:
        num = int(input(prompt))
    except:
        return 0
    return num if num > 0 else 0


print(f"Please give me {N} pairs of positive integers (x,y,z) "
      f"satisfying the equation `x/(y+z) + y/(z+x) + z/(x+y) = {N}`\n")
anss = []
mark = 0
for i in range(N):
    x = read_num("[>] x: ")
    y = read_num("[>] y: ")
    z = read_num("[>] z: ")
    if x * y * z == 0: # positive integer
        mark = 1
        print("This is not what i want!\n")
        break
    if reduce(gcd, [x, y, z]) != 1: # (kx, ky, kz)
        mark = 1
        print("This is not what i want!\n")
        break
    if Frac(x, y+z) + Frac(y, z+x) + Frac(z, x+y) != N:
        mark = 1
        print("This is not what i want!\n")
        break
    ans = tuple(sorted([x, y, z])) # (y, x, z)
    if ans in anss:
        mark = 1
        print("This is not what i want!\n")
        break
    else:
        print("You are right!\n")
        anss.append(ans)
if mark == 0:
    flag = open('flag', 'r').read()
    print("flag is: " + flag + "\n")
else:
    print("Something wrong!\n")

 
 

解题思路

方程化简，转化为二维空间求解（椭圆曲线）。

$$x^3+y^3+z^3-5(x^2y+x^2z+y^2z+z^2y+y^2x+z^2x)-9xyz=0$$

仅仅化成这样还是不够的，需要化成WeierstrassForm模式：

可以将任何场上的椭圆曲线转换成下面的形式：

$$y^2+ay=x^3+bx^2+cxy+dx+e$$

具体转换原理是可以将变量作一个线性变换（可逆的3*3矩阵），转换各变量的最高次数，然后将其中一个变量先固定为1，转换成上述的有理数域的椭圆曲线形式。每个原始方程的整数解（互素），一对一对应于椭圆曲线上的有理点，因此找到整数解就等于在曲线上找到有理点。具体怎么做我们不用考虑细节（论文内有推导），好消息是开源软件sagemath集成了上述转换，总之转换成WeierstrassForm方程后简化了我们计算。更一般的sagemath化成下面的形式(f,g是有理系数)

$$y^2=x^3+fx+g$$

然后有理数域上面的圆锥曲线求解就可以参考ECC了，取一组特解点P（X,Y）不断做切线，不断得到得到nP，注意这些解都是有理数域上面的，从而我们穷举n，可以得到许多组(X,Y,Z)，一直到得到6组这样的正整数解即可，如下图（图源zml博客）。

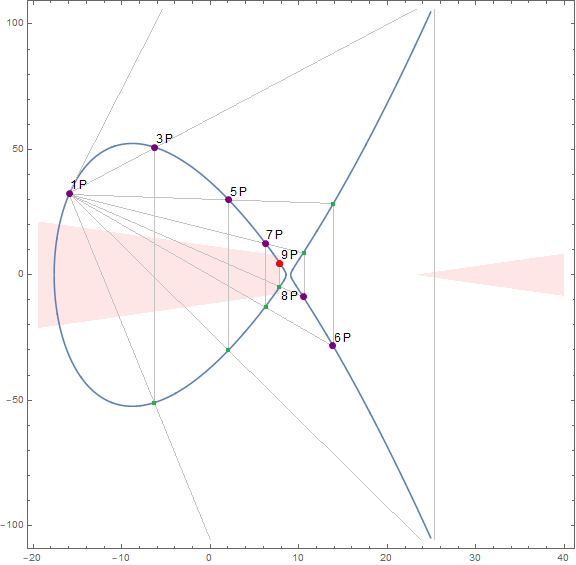
每一组都互素。为了减少穷举量或者最后结果的长度，可以先用python穷举两组无关解，之后再代入求解即可。

<<is_valid>>
<<ec_plus>>
P = S = (-Frac(191, 12), Frac(65, 2))
cnt = 1
while not is_valid(S):
    S = ec_plus(S, P)
    cnt += 1
    print("{}P = ({}, {})".format(cnt, *S))
#源zml博客

 
 

解题脚本（python,sagemath,magma)

上面基于sagemath的代码大都要自己先算一些参数处来（具体的脚本我还没有写，第一次接触sagemath，还在摸索sagemath的一些函数和语法，不过sagemath还是很好用的，现在忙着保研，后面没事了慢慢摸索，想写一个基于任意正整数N的解的脚本）。

下面是在网上看到的基于magma的一个脚本（N=4）。基本逻辑思路注释非常明白了。当时比赛拿的这个脚本改的代码。基本上可以通用N为任意整数的情况的。

// First we define our environment for our "problem" 
 
R<x,y,z> := RationalFunctionField(Rationals(),3); 
 
problem := ((x/(y+z) + y/(x+z) + z/(x+y)) - 6) ; 
// first note that we know a point after some computation (-1,4,11) that 
// works but has a negative coordinate, the following function returns 0, which means that  
// (x/(y+z) + y/(x+z) + z/(x+y)) - 4 = 0    (just put the -4 in the other side) 
Evaluate(problem,[-5, 11, 9]); 
 
// after the previous returned 0 , we know the point fits, we continue. 
 
// we multiply by all the denominators of "problem" to get a polynomials 
problem*Denominator(problem); 
// we obtain a polynomial without denominators x^3 - 3*x^2*y - 3*x^2*z - 3*x*y^2 - 5*x*y*z - 3*x*z^2 + y^3 - 3*y^2*z - 3*y*z^2 + z^3 
// We see is cubic, three variables, and every  term has the same degree (3) , therefore this is a cubic  
// homogeneous curve,  we know there is a point which is not the solution we want 
// the point (-1,4,11) fits in the original "problem" so it should fit in this new curve without denominators too (since no denominator becomes 0) 
 
// We transform this equation to a "curve" in Projecive space of dimension 2 
P2<x,y,z> := ProjectiveSpace(Rationals(),2); 
C := Curve(P2,x^3 - 5*x^2*y - 5*x^2*z - 5*x*y^2 - 9*x*y*z - 5*x*z^2 + y^3 - 5*y^2*z - 5*y*z^2 + z^3); 
 
// fit the point to the curve C (no error is returned) 
Pt := C![-5, 11, 9];
 
// Since all cubic homogeneous curve with at least one point define an elliptc curve, we can transform  
// this curve C to an elliptc curve form and just like in cryptography, we will add this known point (mapped to the corresponded curve) 
// with itself until we get only positive coordinates and go back to C (original Problem) 
 
// Below, E is the curve, f is the map that maps   Points f:C -> E  (C is our original curve without denominators, both curves C,E are equivalent  
// but in E we can "Add points" to get another point of E. 
// and with f^-1 we can return to the point of C which is our original solution 
 
E,f := EllipticCurve(C); 
 
//g is the inverse g:E->C  , f:C->E     so g(f([-1,4,11]))=[-1,4,11] 
g := f^-1; 
 
// We try adding the known point Pt=[-1,4,11] mapped to E, 2..100 times 
// to see if when mapped back the added point to C gives positive coordinates 
//, this is 2*Pt, 3*Pt, ...., 100*Pt  and then mapping back to C all these. 
for n:= 1 to 100 do 
 
// we calculate n times the point of C, known [-1,4,11] but mapped (via f) inside E (where we can do the "n times")  
    nPt_inE:=n*f(Pt); 
 
// we take this point on E back to C via f^-1  (which we renamed as g) 
    nPt_inC:=g(nPt_inE); 
 
//We obtain each coordinate of this point to see if is our positive solution, 
// here MAGMA scales automatically the point such as Z is one always 1,  
// so it puts the same denominators in X,Y, so numerators of X,Y are our  
//solutions and denominator our Z,  think of  P=(a/c,b/c,1)   then c*P=(a,b,c) 
    X := Numerator(nPt_inC[1]); 
    Y := Numerator(nPt_inC[2]); 
    Z := Denominator(nPt_inC[1]); 
 
printf "X=%o\nY=%o\nZ=%o\n",X,Y,Z; 
 
// We check the condition for our original problem. 
  if ((X gt 0) and (Y gt 0)) then 
       printf("GOT IT!!! x=apple, y=banana, z=pineapple, check the above solution\n");  
  else 
     printf "Nee, some coordinate was negative above, I keep in the loop\n\n"; 
  end if; 
 
end for;    
 
// We check the solution fits in the original problem 
if Evaluate(problem, [X,Y,Z]) eq 0 then 
    printf "I evaluated the point to the original problem and yes, it worked!\n"; 
else 
    printf "Mmm this cannot happen!\n"; 
end if; 

 
 
比赛用的的脚本，在线运行magma的网站Magma calculator，但是有个问题是在线环境它输出大于32 MB的时候会截断，并且数字会用/分割，后面再写python脚本把解都存到文件内。通过调输出的整数解的个数刚好可以拿到6组整数解。

R<x,y,z> := RationalFunctionField(Rationals(),3);  
problem := ((x/(y+z) + y/(x+z) + z/(x+y)) - 6) ; 
flag := 0;
Evaluate(problem,[-23, -7, 3]); 
problem*Denominator(problem); 
P2<x,y,z> := ProjectiveSpace(Rationals(),2); 
C := Curve(P2,x^3 - 5*x^2*y - 5*x^2*z - 5*x*y^2 - 9*x*y*z - 5*x*z^2 + y^3 - 5*y^2*z - 5*y*z^2 + z^3); 
Pt := C![-23, -7, 3];
E,f := EllipticCurve(C); 
g := f^-1; 
for n:= 1 to 100 do 
    nPt_inE:=n*f(Pt); 
    nPt_inC:=g(nPt_inE); 
    X := Numerator(nPt_inC[1]); 
    Y := Numerator(nPt_inC[2]); 
    Z := Denominator(nPt_inC[1]); 
    if ((X gt 0) and (Y gt 0)) then
       flag := flag+1;
    end if;  
    printf "X=%o\nY=%o\nZ=%o\n",X,Y,Z;
    if (flag gt 1) and (X gt 0) and (Y gt 0)then //修改该处判断输出对应的正整数解
       printf "GOT IT!!! \nX=%o\nY=%o\nZ=%o\n",X,Y,Z;
    end if; 
 
end for;    
 
if Evaluate(problem, [X,Y,Z]) eq 0 then 
    printf "I evaluated the point to the original problem and yes, it worked!\n"; 
else 
    printf "Mmm this cannot happen!\n"; 
end if; 
//修改问题的方程，代入后再代入两组较小的特解即可，用python在100内爆破就可以拿到两组。

 
 

然后就是我算出结果没拿到flag窒息操作了，注意nc在接受输入过长时会发生截断，因此必须用socket发送数据，可以直接用socket或者pwn包发送。

最后拿到flag如下:

 
 
(sagemath脚本咕咕咕中，这里放一个比赛后看到的大佬的writeup： Lazzaro)