Paper summary - Bootstrapping in FHEW-like Cryptosystems

2023-04-08

字数统计: 1.7k字 | 阅读时长≈ 10分

Reference Paper ：Bootstrapping in FHEW-like Cryptosystems . This blog is a summary of the paper which is the main reference for the BinFHE implementation in OpenFHE. The main contribution is to realize the homomorphic standardized variant of TFHE, that is, to expand the private key sampling range of TFHE from binary $\{0,1\}$ to any sampling range, such as ternary $\{0,1, -1\}$ , and compared FHEW and TFHE when the private key sampling range is the same. Evaluate the bootstrapping speed, bootstrapping key size and other parameters of the two.

Bootstrapping in FHEW-like Cryptosystems 是 OpenFHE 中 BinFHE 实现的主要参考论文。主要贡献在于实现了 TFHE 的同态标准化变体，即将 TFHE 的私钥采样范围从 binary $\{0,1\}$ 扩展到任意采样范围，比如 ternary $\{0,1,-1\}$ ，以及对比了 FHEW 、 TFHE 在私钥采样范围相同时，评估二者的 bootstrapping 速度、bootstrapping key size 等参数。

Basic Ring LWE

Annotations

Let $R=\mathbb{Z}[X] /\left(X^n+1\right)$ be the $2 n$ th cyclotomic ring, for $n=2^k$ , and $R_q=R / q R \equiv \mathbb{Z}_q[X] /\left(X^n+1\right)$ . We identify ring elements with the corresponding coefficient vectors in $\mathbb{Z}^n$ and $\mathbb{Z}_q^n$ .
Encoding of $m$ in MSB : encode $m \in R_t$ as $\tilde{m}=(q / t) m$ .
Decoding arbitrary $x$ :
$f(x)=\lfloor(t / q) x\rceil \quad(\bmod t)$
Basic Ring LWE symmetric encryption of (the encoding of) a message $\tilde{m} \in R_q$ under key $s \in R$ as：
$\operatorname{RLWE}_s(\tilde{m})=(a, a s+e+\tilde{m})$
where $a \leftarrow R_q$ is chosen uniformly at random, and $e \leftarrow \chi_\sigma^n$ is chosen from a discrete Gaussian distribution of parameter $\sigma$ . Also marked as $\operatorname{RLWE}_s(\tilde{m} ; a, e)$ or $\operatorname{RLWE}_s(\tilde{m} ; e)$
Decryption of Ring LWE ：
$\operatorname{RLWE}_s^{-1}(a, b)=b-a s=\tilde{m}+e$
Homomorphic multiplication operation (allowed only when d is small)
$(\cdot): R \times \mathrm{RLWE} \rightarrow \mathrm{RLWE}$

Basic RGSW

Annotations

Vector of basis decomposition Ring LWE (also called RLEV):
$\operatorname{RLWE}_s^{\prime}(m)=\left(\operatorname{RLWE}_s(m), \operatorname{RLWE}_s(B m), \operatorname{RLWE}\left(B^2 m\right), \ldots, \operatorname{RLWE}_s\left(B^{k-1} m\right)\right)$
where the base $B$ is usually small enough to support homomorphic multiplication between large ciphertext.
Homomorphic multiplication operation with large $d=\sum_i B^i d_i$ with $B$ -bounded component polynomials $d_i$ :
$(\odot): R \times \mathrm{RLWE}^{\prime} \rightarrow \mathrm{RLWE} \\ d \odot\left(\mathbf{c}_0, \ldots, \mathbf{c}_{k-1}\right)=\sum_i d_i \cdot \mathbf{c}_i .$
RGSW Ciphertext ：
$\operatorname{RGSW}_s(m)=\left(\operatorname{RLWE}_s^{\prime}(-s \cdot m), \operatorname{RLWE}_s^{\prime}(m)\right) \tag{1}$
Magic Properties :

Trivial ciphertext of s : $(-1,0)$ .

No secret information form of $\operatorname{RLWE}_s^{\prime}(-s \cdot m)$ :
$\operatorname{RLWE}_s^{\prime}(-s \cdot m)=\operatorname{RLWE}_s^{\prime}(0)-m \cdot(-1,0)=(a+m, a s+e)$
Also $\operatorname{RGSW}_s(m)$ ciphertexts can be equivalently written as
$\operatorname{RGSW}_s(m)=\left(\operatorname{RLWE}_s(0), \ldots, \operatorname{RLWE}_s(0)\right)+m \mathbf{G} \tag{2}$
where $\mathbf{G}=\mathbf{I} \otimes\left(1, B, B^2, \ldots, B^{k-1}\right)$ is the powers-of-B “gadget matrix”. For simplicity, PALISADE implements the RGSW cryptosystem directly using equation (2), but multiplication between RGSW ciphertexts is best analyzed using the modular definition (1).

Homomorphic Multiplication

Given $(a, b)=\operatorname{RLWE}_s\left(m_0 ; e_0\right)$ and $\left(\mathbf{c}, \mathbf{c}^{\prime}\right)=\operatorname{RGSW}_s\left(m_1\right)$ one computes

$\begin{aligned} (a, b) \diamond\left(\mathbf{c}, \mathbf{c}^{\prime}\right) & =\left\langle(a, b),\left(\mathbf{c}, \mathbf{c}^{\prime}\right)\right\rangle \\ & =a \odot \mathbf{c}+b \odot \mathbf{c}^{\prime} \\ & =a \odot \operatorname{RLWE}_s^{\prime}\left(-s \cdot m_1\right)+b \odot \operatorname{RLWE}_s^{\prime}\left(m_1\right) \\ & =\operatorname{RLWE}_s\left(-s \cdot a \cdot m_1\right)+\operatorname{RLWE}_s\left(b \cdot m_1\right) \\ & =\operatorname{RLWE}_s\left(b \cdot m_1-a \cdot s \cdot m_1\right) \\ & =\operatorname{RLWE}_s\left((b-a s) \cdot m_1\right) \\ & =\operatorname{RLWE}_s\left(m_0 m_1+e_0 m_1\right) . \end{aligned}$

This is an encryption of the product $m_0 m_1$ , with an additional error term $e_0 m_1$ . For this operation to be effective, RGSW encryption is usually restricted to small messages $m_1$ , typically $m_1= \pm X^v$ , so that $\left\|e_0 m_1\right\|=\left\|e_0\right\|$ . This multiplication operation has type

$(\diamond): \text { RLWE } \times \text { RGSW } \rightarrow \text { RLWE }$

Extended component-wise :

$\begin{aligned} (\diamond): \mathrm{RLWE}^{\prime} \times \mathrm{RGSW}_{\rightarrow} \rightarrow \mathrm{RLWE}^{\prime} \quad\left(\mathbf{c}_0, \ldots, \mathbf{c}_{k-1}\right) \diamond \mathbf{C} & =\left(\mathbf{c}_0 \diamond \mathbf{C}, \ldots, \mathbf{c}_{k-1} \diamond \mathbf{C}\right) \\ (\diamond): \mathrm{RGSW} \times \mathrm{RGSW} \rightarrow \mathrm{RGSW} \quad\left(\mathbf{c}, \mathbf{c}^{\prime}\right) \diamond \mathbf{C} & =\left(\mathbf{c} \diamond \mathbf{C}, \mathbf{c}^{\prime} \diamond \mathbf{C}\right) \end{aligned}$

Bootstrapping*

Usually, bootstrapping is processed on $\textsf{LWE}$ ciphertexts having the form $(\mathbf{a}, b)$ where $\mathbf{a} \in \mathbb{Z}_q^n$ and $b \in \mathbb{Z}_q$ , and keys are vectors $\mathbf{s} \in \mathbb{Z}_q^n$ , possibly chosen from a subset of $\mathbb{Z}_q^n$ .

The core component : cryptographic accumulator $\mathrm{ACC}$ .

Initialize: $\mathrm{ACC} \leftarrow b$ , setting the content of ACC to any known value $b \in \mathbb{Z}_q$
Update: ACC $\pm c \cdot E(s)$ , modifying the content of the accumulator from $\operatorname{ACC}[v]$ to $\mathrm{ACC}[v+$ $c \cdot s]$ , where $c, s \in \mathbb{Z}_q$ , and $s$ is given encrypted under $E$ .
Extract: $f(\mathrm{ACC})$ , returning an encryption $\tilde{E}(f(v))$ of function $f$ applied to the current content of the accumulator ACC $[v]$ .

The key for bootstrapping is called evaluation key , refreshing key, bootstrapping key and etc.

$\mathrm{ek}=E(\mathbf{s})=\left(E\left(s_1\right), \ldots, E\left(s_n\right)\right)$

High-level procedure : decryption by $\textsf{ACC}$ and rounding by $f$ .

FHEW/TFHE Bootstrapping :

FHEW : The AP bootstrapping procedure [4] supports basic updates ACC $\leftarrow E(s)$ for arbitrary $s \in \mathbb{Z}_q$ . Then, ACC $\leftarrow c \cdot E(s)$ is implemented by providing (in the bootstrapping key) encryptions $E\left(2^i s\right)$ of multiples of the secret key elements $s$ , taking the binary expansion of $c=\sum_i 2^i c_i$ , and then executing ACC $\stackrel{+}{\leftarrow}\left(2^i s\right)$ for all $i$ such that $c_i=1$ .
TFHE/CGGI : The GINX bootstrapping procedure [24] supports basic updates ACC $\leftarrow c \cdot E(s)$ where $c \in \mathbb{Z}_q$ is arbitrary, but $s \in\{0,1\}$ is a single bit. Then, for an arbitrary secret $s=\sum_i 2^i s_i \in \mathbb{Z}_q$ , one can execute ACC $\stackrel{+}{\leftarrow}\left(2^i c\right) \cdot E\left(s_i\right)$ for all $i$ .

Features :

AP has a time-space trade-off. $a=\sum_i B_{\mathrm{r}}{ }^i a_i$ is written to a base $B_{\mathrm{r}} \geq 2$ (with digits $a_i \in \mathbb{Z}_{B_{\mathrm{r}}}$ ), and the bootstrapping key includes encryptions $E\left(B_{\mathrm{r}}{ }^i a s\right)$ for all $i \leq \log _{B_{\mathrm{r}}} q$ and $a \in \mathbb{Z}_{B_{\mathrm{r}}}$ .
Only support binary expansion of the secret key $s=\sum_i 2^i s_i$ .

Ring LWE Accumulators*

The last section does not involve details of the cryptographic accumulator and here we will introduce the designing of Ring LWE accumulators which makes the rounding function $f$ trivial and fast.

The main idea of the FHEW accumulators ：work in a cyclotomic ring of order $q$ , and represent values $v \in \mathbb{Z}_q$ as $X^v \in \mathbb{Z}[X] / \Phi_q(X)$ , where $\Phi_q(X)$ is the $q$ th cyclotomic polynomial. Since $X$ has multiplicative order $q$ in $\mathbb{Z}[X] / \Phi_q(X)$ , addition in the exponent of $X^v$ is performed modulo $q$ . Following [20], we assume $q=2^k$ is a power of 2 , and use the ring $R_Q=\mathbb{Z}_Q[X] /\left(X^{q / 2}+1\right)$ for a sufficiently larger modulus $Q$ .

The ring $R_Q$ is used to implement the RLWE, RLWE’ and RGSW encryption schemes . The smaller modulus $q$ is only used for the LWE ciphertext given as input to the bootstrapping procedure.

Points

The ciphertext modulus $q$ is only used for LWE ciphertext!
RLWE, RLWE’ and RGSW modulus is $Q$ .
Polynomial quotient : $X^N + 1$ where $N > q/2$
Embed the ring $\mathbb{Z}_Q[X] /\left(X^{q / 2}+1\right)$ into $\mathbb{Z}_Q[X] /\left(X^N+1\right)$

FHEW/CGGI accumulators

Store the value $v \in \mathbb{Z}_q$ as $\operatorname{ACC}[v]=\operatorname{RGSW}\left(X^v\right)$ . And the programmable function must satisfy :
$f(v+(q / 2))=-f(v)$
If the function $f$ is known in advance, the value $v$ can be alternatively stored as
$\operatorname{ACC}[v]=\operatorname{RGSW}\left(\sum_{i=0}^{q / 2-1} f(v-i) \cdot X^i\right)$
If only an LWE ciphertext is needed at the end of the computation, one can set the accumulator :
$\operatorname{ACC}[v]=\operatorname{RLWE}\left(X^v\right)$
The final version in practice :
$\operatorname{ACC}[v]=\operatorname{RLWE}\left(\sum_{i=0}^{q / 2-1} f(v-i) \cdot X^i\right)$

Init ACC and Extract LWE Ciphertext

FHEW : AP Update

The update operation is the most complicated and expensive in bootstrapping and it differs among the two homomorphic cryptosystems. This section focuses on the FHEW ACC Update.

In $\mathrm{AP} \text{ of } \mathrm{FHEW}$ , each secret value $s \in \mathbb{Z}_q$ is encrypted as

$E(s)=\left\{\mathbf{Z}_{j, v}=\operatorname{RGSW}\left(X^{v B_{\mathrm{r}}{ }^j \cdot s}\right) \mid j<\log _{B_{\mathrm{r}}} q, v \in \mathbb{Z}_{B_{\mathrm{r}}}\right\} .$

The updating process $\operatorname{ACC}[v] \stackrel{+}{\leftarrow} c \cdot E(s)$ where $c \in \mathbb Z_q$ :

Decompose with base $B_r$ : $c=\sum_i B_{\mathrm{r}}{ }^i c_i$
ACC $:=\mathrm{ACC} \diamond \mathbf{Z}_{j, c_j}$ for $j=0, \ldots, \log _{B_{\mathrm{r}}} q-1$ , using the RLWE $\times$ RGSW $\rightarrow$ RLWE multiplication operation.

Combine things together , how does cryptographic accumulator change during bootstrapping with LWE ciphertext being $(\vec {\mathbf a},b) \in \mathbb Z_q^{n+1}$ ?

Init ACC ( Init LUT polynomial, rotated by $b \in \mathbb Z_q$ ):
$\operatorname{ACC}[v]=\operatorname{RLWE}\left(\sum_{i=0}^{q / 2-1} f(v-i) \cdot X^i\right)$
From a homomorphic perspective : $\operatorname{ACC} = LUT \cdot X^{-b}$
Update ACC $n$ times, in each step:
$\operatorname{ACC} :=\mathrm{ACC} \diamond \mathbf{Z}_{j, c_j} \quad for \ j=0, \ldots, \log _{B_{\mathrm{r}}} q-1$
From a homomorphic perspective : $\operatorname{ACC} = \mathrm{ACC} \cdot X^{a_i \cdot s_i}$

After n times update : $\operatorname{ACC} = LUT \cdot X^{ -(b - \sum_0^{n} a_i \cdot s_i)}$
Extract the constant , from a homomorphic perspective :
$f(b - \sum_0^{n} a_i \cdot s_i) = f(m+ \Delta) = f(m)$
since the LUT maps all valid $f(m+ \Delta)$ in mega-case to $f(m)$ .

TFHE/CGGI : GINX Update

In $\mathrm{GINX} \text{ of } \mathrm{FHEW}$ , each secret value $s \in \mathbb{Z}_q$ is encrypted as :

Decompose $s$ : each secret value $s \in \mathbb{Z}_q$ needs to be expressed as a subset-sum $s=\sum_{u \in U} u$ . $x_u$ (with $x_u \in\{0,1\}$ ) where $U \subset \mathbb{Z}_q$ is an appropriate subset of $\mathbb{Z}_q$ ( if $s$ is sampled in $\{0,1\}$ , $U = \{1\}$ ).
For any such $U$ , the secret encryption function is defined as
$\begin{gathered} E^{\prime}(s)=\left\{\mathbf{Z}_u=\operatorname{RGSW}\left(x_u\right) \mid \text { for some } \mathbf{x} \in\{0,1\}^U\right. \\ \text { such that } \left.\sum_u u \cdot x_u=s\right\} . \end{gathered}$

The update operation $\operatorname{ACC}[v] \stackrel{+}{\leftarrow} c \cdot E(s)$ is computed by sequentially updating

$\mathrm{ACC}:=\mathrm{ACC} \diamond \overline{\mathbf{Z}}_u+\left(X^{u \cdot c} \cdot \mathrm{ACC}\right) \diamond \mathbf{Z}_u$

for $u \in U$ , where

$\overline{\mathbf{Z}}_u=\mathbf{G}-\mathbf{Z}_u=\operatorname{RGSW}(1)-\mathbf{Z}_u$

A faster version which takes only one homomorphic multiplication is :

$\mathrm{ACC}:=\mathrm{ACC}+\left(X^{u \cdot c}-1\right)\left(\mathrm{ACC} \diamond \mathbf{Z}_u\right)$

Combine things together , how does cryptographic accumulator change during bootstrapping with LWE ciphertext being $(\vec {\mathbf a},b) \in \mathbb Z_q^{n+1}$ ?

Init ACC ( Init LUT polynomial, rotated by $b \in \mathbb Z_q$ ):
$\operatorname{ACC}[v]=\operatorname{RLWE}\left(\sum_{i=0}^{q / 2-1} f(v-i) \cdot X^i\right)$
From a homomorphic perspective : $\operatorname{ACC} = LUT \cdot X^{-b}$
Update ACC $n$ times, in each step:
$\mathrm{ACC}:=\mathrm{ACC}+\left(X^{u \cdot c}-1\right)\left(\mathrm{ACC} \diamond \mathbf{Z}_u\right)$
From a homomorphic perspective : $\operatorname{ACC} = \mathrm{ACC}\cdot X^{a_i \cdot s_i}$

After n times update : $\operatorname{ACC} = LUT \cdot X^{ -(b - \sum_0^{n} a_i \cdot s_i)}$
Extract the constant , from a homomorphic perspective :
$f(b - \sum_0^{n} a_i \cdot s_i) = f(m+ \Delta) = f(m)$
since the LUT maps all valid $f(m+ \Delta)$ in mega-case to $f(m)$ .

Summary

The two bootstrapping processes differ in the update operation.

The FHEW/AP decomposes the ciphertext with certain pre-determined base . Thus , we do not require the secret key distribution to be binary . Here we briefly discuss the time-space trade-off.
1. The bootstrapping decomposition base $B_r$ is large : then the bootstrapping key size will be smaller but the $(\diamond): \text { RLWE } \times \text { RGSW } \rightarrow \text { RLWE }$ product increases thus increasing the bootstrapping time !
2. The secret key distribution has no influences in the the bootstrapping key size and running time.
The TFHE/GINX decomposes the secret key with subset $U \subset \mathbb Z_q$ . Specifically, the initial TFHE utilizes the binary distribution which maximally eliminates the running time but sacrifices the security level. All the variants of TFHE relies on the CMux gate with the choice bit being the secret and therefore, they demands the private key to be encrypted bit by bit which means the plaintext of $\textsf{RGSW(m)}$ must belong to $\{0,1\}$ .

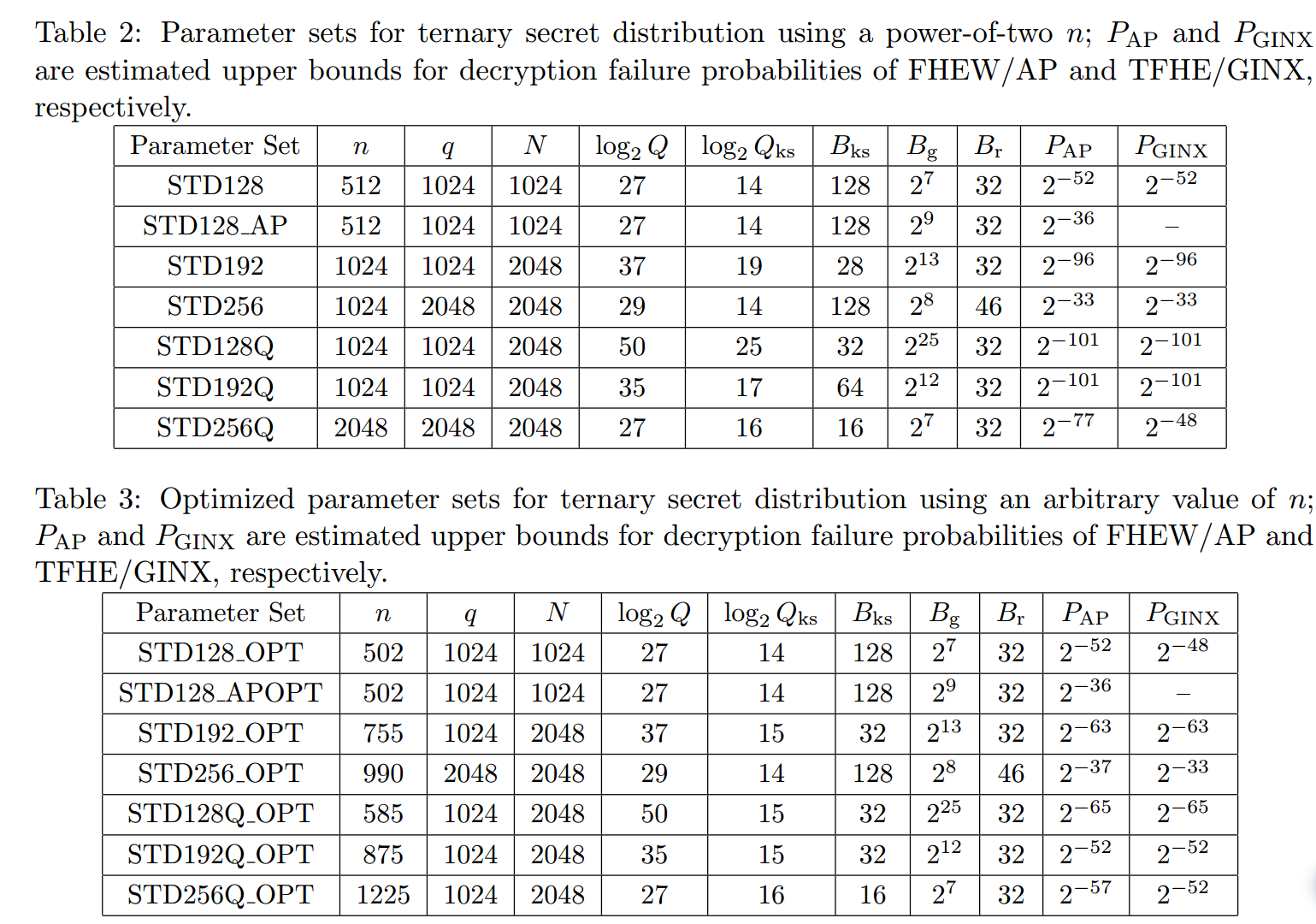
Some parameters

$q$ , small (LWE) modulus;
$n$ , lattice parameter for the LWE scheme;
$Q$ , RLWE/RGSW modulus used in the core bootstrapping procedure based on an accumulator;
$Q_{\mathrm{ks}}$ , LWE/RLWE modulus used for key switching;
$N$ , ring dimension for RLWE/RGSW;
$B_{\mathrm{g}}$ , gadget base for digit decomposition in each accumulator update, which breaks integers $\bmod Q$ into $d_{\mathrm{g}}$ digits;
$B_{\mathrm{ks}}$ , gadget base used for key switching, which breaks integers $\bmod Q$ into $d_{\mathrm{ks}}$ digits;
$B_{\mathrm{r}}$ , gadget base in FHEW/AP (not used in TFHE/GINX), which breaks integers $\bmod q$ into $d_{\mathrm{r}}$ digits.

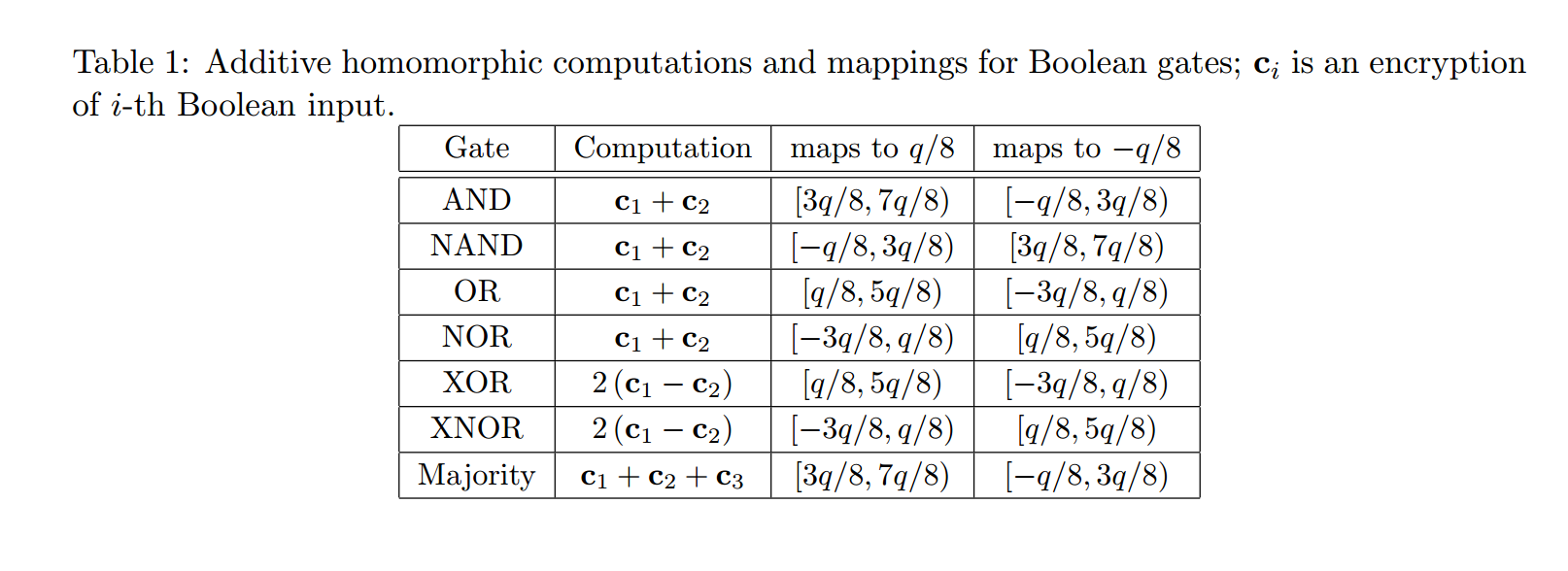
Homomorphic Rounding and Bitwise Gate

We conclude with a discussion of the function $f$ used by the extraction function at the end of bootstrapping.

NAND Gate

The NAND of two ciphertexts $\left(\mathbf{a}_0, b_0\right)=\operatorname{LWE}\left(m_0(q / 4)\right)$ and $\left(\mathbf{a}_1, b_1\right)=\operatorname{LWE}\left(m_1(q / 4)\right)$ .
Homomorphic Addition : obtain an encryption $(\mathbf{a}, b)=\left(\mathbf{a}_0+\mathbf{a}_1, b_0+b_1\right)$ of $m_0+m_1 \in$ $\{0,1,2\}$ with noise less than $\left|e_0+e_1\right|<q / 8$ .
Bootstrapping : ciphertext $(\mathbf{a}, b)=\operatorname{LWE}\left(\left(m_0+m_1\right)(q / 4)\right)$ is homomorphically decrypted using the bootstrapping procedure .

Rounding functions implemented by the $f$ function ( Look-Up table ) :

Rounds $m+e=\left(m_0+m_1\right)(q / 4)+\left(e_0+e_1\right)$ to the closest multiple of $q / 4$ , then
maps $0 \mapsto 1,1 \mapsto 1,2 \mapsto 0$ , (and, for completeness, also $3 \mapsto 0$ )
finally multiplies the resulting bit by the scaling factor $Q / 4$ . (Remember that the extraction procedure returns an LWE ciphertext modulo $Q$ . A ciphertext modulo $q$ can be obtained using key/modulus switching.)

Other bitwise gates :

The process :

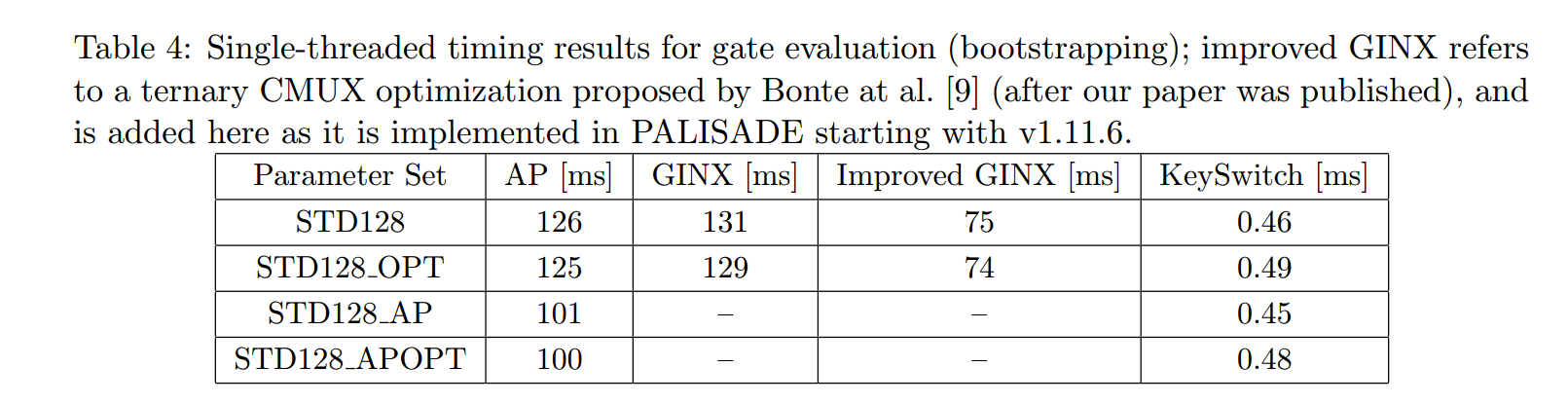
Implementation Results

The latest acceleration updated in 2022 Oct (paper).